作者:丁尹

今天阅读的这篇文献是复旦大学航空航天系的作品,Emmm,之前看到他们作品的次数比较少,所以乍一看到这个题目我还很惊奇,这个“老生常谈”的主题竟然也有SCI的潜力?
不过仔细读下去,确实看到了一些还不错的内容。
本文关键词:动量叶素理论、CFD方法、人工神经网络、旋翼配平方法
直升机旋翼CFD配平的难题
众所周知,即便在计算机性能大幅提升的当今之世,计算流体力学(CFD)仍然是一项对计算资源要求相当高的流体求解技术(毕竟不是谁都能用上超算中心的)。这个问题在直升机旋翼的计算中就更加突出了,毕竟旋翼不仅在旋转,还得要变距、挥舞,由此就需要运动嵌套网格、滑移网格、挖洞什么的一系列技术,这都进一步增加了计算资源的消耗,使得直升机旋翼CFD的计算效率始终处于一个较低的水平。
而且一旦涉及到配平,那么直升机旋翼CFD的计算效率将会随着配平迭代次数的增加而更进一步降低。为了解决这个很现实的问题,研究人员开发了一种松耦合的异步式配平方法,这种方法的特点就是一套系统包含两组模型——一组低精度算的快、一组高精度算的慢——首先用低精度模型快速迭代配平,得到初始解,或者一个Jacobian矩阵,随后再放到高精度模型里面去异步求解。
不支持在 Docs 外粘贴 block
▲异步式配平方法的流程示意图
尽管在早期的旋翼CFD中涉及了类似的方法[1],不过这种求解算法是FLIGHTLAB的作者赵景根在将黏性涡粒子方法应用到旋翼气动干扰分析中的时候系统提出来的[2],该方法被赵景根叫做“Delta Method“,我第一次看到该方法则是魏鹏在他的博士学位论文(导师徐国华教授)中详细介绍了这种方法[3],并将其叫做”差量法“,随后在徐国华的学生的一系列涉及旋翼CFD配平方法的论文中采用了这种方法[4-5],徐明的博士论文(导师李建波教授)中也基于这种技术在动态入流和自由尾迹之间搭建了桥梁,进行了转速优化旋翼的气动布局设计研究[6],段登燕也将该方法应用到了多个无人直升机组合作业的干扰流场分析中[7],足见该方法在旋翼高精度气动模型的配平中相当有效。
Weili Lyu的研究创新点在哪里?
看完我上面所说的内容,想必大家会有一种感觉,这个直升机混合配平方法都已经被这么多人用过了,高精度模型也涉及到了黏性涡粒子方法、CFD方法、自由尾迹方法等,那这个方法还有什么地方可以创新呢?
Lyu(抱歉不熟悉这位作者,只能用英文名😂)想了一个特别的思路——既然高精度模型这条路已经走不通了,那我就从低精度模型入手,做一些创新点吧——所以,他这篇论文的主要创新点是从低精度模型出发的。
他的混合配平算法的本质是动量叶素理论(BEM)和CFD模型的耦合,众所周知,BEM方法的置信度很大程度上是取决于桨叶的翼型文件的,如果翼型数据表非常准确的话,BEM方法模型的计算精度可以做到媲美CFD这种高精度方法[8]。但是,“非常准确的翼型数据表”对应的是什么?
是风洞实验室、加工精度很高的特定翼型的桨叶、大量复杂的高精度实验设备和经验丰富的实验人员,由此可见,非常准确的翼型数据表的绘制是一项非常复杂的工作,那么,如果退而求其次呢?可以用CFD软件,比如说Fluent之类,或者大名鼎鼎的Xfoil[9]进行预先计算,尽管这两种方法都已经得到了足够的验证,但是要用Fluent准备一份涵盖大量雷诺数、马赫数、迎角情况的翼型数据表,并不是一件容易的事情;而用Xfoil进行计算的话,看起来似乎简单一些,但是在一些特别的状态,比如说低雷诺数、高马赫数等情况,其计算收敛性比较差,经常要非常仔细的调整,而且每用到一种翼型就需要用Xfoil计算一次,其所需要的工作量也没有想象中那么小。
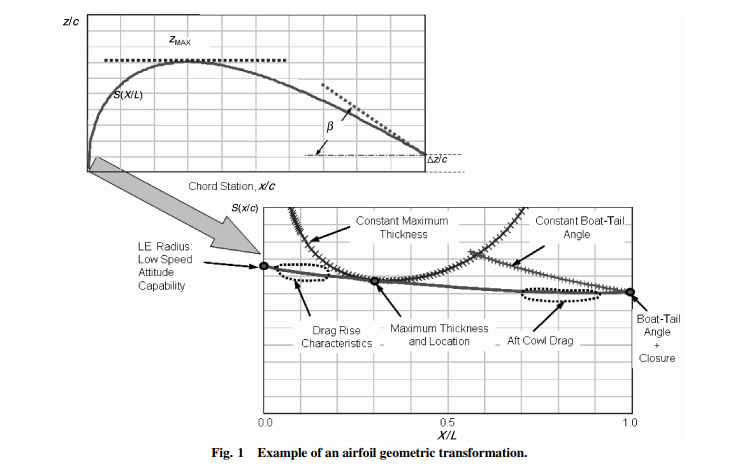
主要就是针对上述的这个问题,Lyu发展了一种用人工神经网络来进行翼型气动力系数计算的方法,方法细节大家可以查阅原论文,我描述一下他的总体思路:输入量就是一个描述翼型轮廓的形函数[10]、迎角、马赫数和雷诺数,输出量就是升力系数和阻力系数。
▲翼型几何形状转换为形函数[10]
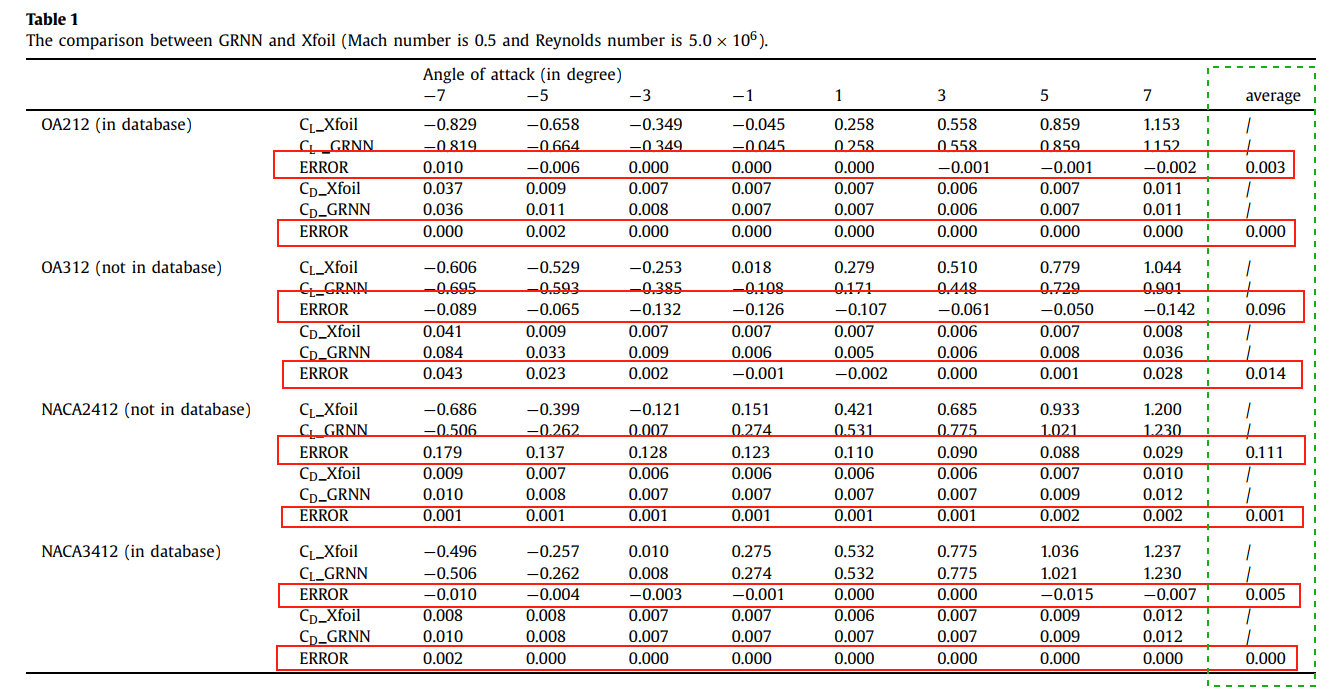
他用30多组包含有对称和非对称的直升机桨叶翼型(包含NACA系列,OA系列,SC系列、RAE系列和VR系列)建立了数据库,其气动力是通过Xfoil进行预先计算的,最后的计算结果如下图所示,从图中可以看出,这套模型的预测结果并不是非常优秀,但确实也提供了一个新的思路。
不过话说回来,关于神经网络方法在翼型气动系数方面的预测,相关的研究在十多年前就有了😂,Mailema Celestino dos Santos在2008年的AIAA Aerospace Sciences Meeting and Exhibit上,就以题为的文章解释了这种翼型气动力预测技术,并取得了不错的结论[11];2009年,Dilek Funda Kurtulus也发表了相关的研究,用人工神经网络预测了翼型的非定常气动力[12];2017年,陈海在发表的论文中直接基于翼型的图像进行了翼型法向力系数的研究,得出了正面的结论[13];近年来,相关的研究更多[14-15]。
Lyu的优势大概是他把这种方法模型和直升机旋翼的差量配平那一套结合起来了,面向直升机旋翼配平的实用价值和意义更大一些。
参考文献
Strawn R C, Caradonna F X. Conservative full-potential model for unsteady transonic rotor flows[J]. AIAA journal, 1987, 25(2): 193-198.
ZHAO J, HE C, 2010. A Viscous Vortex Particle Model for Rotor Wake and Interference Analysis[J]. Journal of the American Helicopter Society, 55(1): 12007–1200714. DOI:10.4050/JAHS.55.012007.
魏鹏, 2012. 旋翼非定常流场的黏性涡数值模拟方法及其混合方法的研究[D]. 南京航空航天大学.
Qi H, Xu G, Lu C, et al. A study of coaxial rotor aerodynamic interaction mechanism in hover with high-efficient trim model[J]. Aerospace Science and Technology, 2019, 84: 1116-1130.
Ye Z, Xu G, Shi Y, et al. A high-efficiency trim method for CFD numerical calculation of helicopter rotors[J]. International Journal of Aeronautical and Space Sciences, 2017, 18(2): 186-196.
徐明. 最优转速旋翼直升机总体气动技术研究[D]. 南京航空航天大学, 2016.
Duan D, Wang Z, Li J, et al. Stabilization control for unmanned helicopter-slung load system based on active disturbance rejection control and improved sliding mode con-trol[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aer-ospace Engineering, 2021: 0954410020985157.
Ning S A. A simple solution method for the blade element momentum equations with guaranteed convergence[J]. Wind Energy, 2014, 17(9): 1327-1345.
Drela M. XFOIL: An analysis and design system for low Reynolds number airfoils[M]//Low Reynolds number aerodynamics. Springer, Berlin, Heidelberg, 1989: 1-12.
Kulfan B M. Universal parametric geometry representation method[J]. Journal of aircraft, 2008, 45(1): 142-158.
Santos M, Mattos B, Girardi R. Aerodynamic coefficient prediction of airfoils using neural networks[C]//46th AIAA aerospace sciences meeting and exhibit. 2008: 887.
Kurtulus D F. Ability to forecast unsteady aerodynamic forces of flapping airfoils by artificial neural network[J]. Neural Computing and Applications, 2009, 18(4): 359-368.
Chen H, Qian W Q, He L. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta AerodynamicaSinica, 2018, 36(2): 294G299.
Balla K, Sevilla R, Hassan O, et al. An application of neural networks to the prediction of aerodynamic coefficients of aerofoils and wings[J]. Applied Mathematical Modelling, 2021, 96: 456-479.
Zhu L, Zhang W, Sun X, et al. Turbulence closure for high Reynolds number airfoil flows by deep neural networks[J]. Aerospace Science and Technology, 2021, 110: 106452.